Updated 12 August 2024

Published 9 August 2024

Exchange interaction

We are going to use the concept of exchange energy to demonstrate why two electrons interacting via their Coulomb interaction prefer to have their spins parallel rather than anti-parallel, assuming all other factors are equal.

This preference arises from the quantum mechanical principle that the total wavefunction of two indistinguishable fermions (such as electrons) must be antisymmetric with respect to the exchange of particles. This principle leads to the Pauli exclusion principle, which states that no two electrons can occupy the same quantum state simultaneously.

When two electrons have parallel spins ( $\uparrow\uparrow$ ), the spatial part of their wavefunction must be anti-symmetric to satisfy the antisymmetry of the total wavefunction. An anti-symmetric spatial wavefunction reduces the overlap between the electron wavefunctions, which in turn reduces the Coulomb repulsion between them. This reduced repulsion lowers the total energy of the system, leading to a situation where:

$E(\uparrow\uparrow ) < E(\uparrow\downarrow )$

The energy difference between these two configurations is known as the exchange energy. The exchange energy is a quantum mechanical effect with no classical analog, and it is a direct consequence of the antisymmetry requirement for fermions.

1. Stating the problem

The first excited state of a Helium atom is a straightforward example to consider because it only involves two electrons. We focus on the first excited state to compare the energy configurations of parallel versus anti-parallel spins when one electron is in the $1s$ orbital and the other is in the $2s$ orbital. By examining these configurations, we can determine which one has the lower energy.

In the ground state of the Helium atom, both electrons occupy the $1s$ orbital. In this configuration, the Pauli exclusion principle requires the spins to be anti-parallel, so it is not possible to compare parallel and anti-parallel spin configurations in the ground state

The Hamiltonian for a system with two interacting electrons can be decomposed into the following terms:

$\mathcal{H} = \mathcal{H}_1 + \mathcal{H}_2 + \mathcal{H}_{12}$

where,

$\mathcal{H}_1$ represents the hamiltonian for electron 1, assuming it is the only electron present. It consists of the kinetic energy and the potential energydue to the Coulomb interaction between electron 1 and the nucleus. This is given by:
$\mathcal{H}_1=\frac{-\hbar}{2m}\nabla_1^2 - \frac{Ze^2}{4\pi\varepsilon_0r_1}$
In this term, $r_1$ is the distance of electron 1 from the nucleus.
$\mathcal{H}_2$ has the same form,but it describes the kinetic and potential energy for electron 2:
$\mathcal{H}_2=\frac{-\hbar}{2m}\nabla_2^2 - \frac{Ze^2}{4\pi\varepsilon_0r_2}$ .
If the electrons did not interact with each other, the total Hamiltonian would simply be the sum of $\mathcal{H}_1$ and $\mathcal{H}_2$ . However, because the electrons do interact, there is an additional term;
$\mathcal{H}_{12}$ represents the Coulomb interactions between the two electrons.
$\mathcal{H}_{12}=\frac{e^2}{4\pi\varepsilon_0r_{12}}$
This term is positive because the interaction is repulsive (both electrons have the same negative charge). Here, $r_{12} = |r_1-r_2$ is the distance between the two electrons.

To calculate the energy of this system, we need to take the expectation value of the Hamiltonian with respect to the electronic wave function, $\psi(r_1, r_2)$ , which depends on the positions of both electrons:

$E = <\psi(r_1, r_2)|\mathcal{H}|\psi(r_1, r_2)>$

We are interested in calculating the energy for the cases where the spins of the electrons are parallel and where they are anti-parallel.

2. Energy of the system

The Pauli exclusion principle states that any atomic or molecular orbital can accommodate a maximum of two electrons, and these electrons must have opposite spins. A more rigorous expression of the Pauli principle is that the total electronic wave function must be antisymmetric with respect to the exchange of any two electrons.

In our specific problem involving two electrons, the wave function must change sign when the electrons are swapped. The wave function $\psi$ is composed of a spatial part, dependent on the positions of electrons 1 and 2, and a spin part, dependent on the orientation of their spins. Thus, there are two configurations of the wave function for two electrons that adhere to the Pauli principle:

A symmetric spin part with an antisymmetric spatial part.
An antisymmetric spin part with a symmetric spatial part.

A symmetric spin part means that the spin part of the wave function remains unchanged when the spins of the two electrons are exchanged. This occurs when the electron spins are parallel. In contrast, an antisymmetric spin part means that swapping the spins of the two electrons results in the spin part of the wave function changing sign. This happens when the electron spins are antiparallel.

The spatial parts of the wave function (symmetric and antisymmetric) correspond to these different spin arrangements. In summary, when the spins are parallel, the spatial part of the wave function must be antisymmetric, and when the spins are antiparallel, the spatial part must be symmetric.

2.1 Symmetric spin part

For the spin part to be symmetric ( $\uparrow\uparrow$ ), the spatial part of the wave function has to be anti-symmetric. The way that we can make an anti-symmetric wave function of electron 1 and electron 2, is to put electron 1 in the $1s$ orbital, and electron 2 in the $2s$ orbital ( $\phi_{1s}(r_1)\phi_{2s}(r_2)$ ). Of course we can equally likely have electron 1 in the $2s$ and electron 2 in the $1s$ orbital ( $\phi_{2s}(r_1)\phi_{1s}(r_2)$ ). We can write this in the following way:

$\psi(r_1, r_2) = \frac{1}{\sqrt{2}}\left[\phi_{1s}(r_1)\phi_{2s}(r_2) - \phi_{2s}(r_1)\phi_{1s}(r_2)\right]$

where the root 2 is to normalize it. Furthermore, he minus sign in between is to make the wave function anti-symmetric. If I exchange electron 1 with electron 2, the wave function as a whole changes sign. You’d end up with:

$\psi(r_1, r_2) = \frac{1}{\sqrt{2}}\left[\phi_{2s}(r_1)\phi_{1s}(r_2)-\phi_{1s}(r_1)\phi_{2s}(r_2)\right]$

2.2 Anti-symmetric spin part

For the anti-symmetric spin part ( $\uparrow\downarrow$ ), we can write down the symmetric spatial part of the same form as follows:

$\psi(r_1, r_2) = \frac{1}{\sqrt{2}}\left[\phi_{1s}(r_1)\phi_{2s}(r_2) + \phi_{2s}(r_1)\phi_{1s}(r_2)\right]$

Now we see a plus sign, so that means if I swap electron 1 with electron 2, this spatial part of the wave function remains unchanged. It is symmetric with respect to the exchange of electron 1 and 2.

3. Solving the expectation value

Given that we have two spatial wave functions, we can now work out the energy in the two cases ( $\uparrow\uparrow$ versus $\uparrow\downarrow$ ).

$\begin{aligned}E & =\ < \psi(r_1, r_2) |\mathcal{H}|\psi(r_1, r_2)>\\ & = \frac{1}{2}<\left[\phi_{1s}(r_1)\phi_{2s}(r_2) \pm \phi_{2s}(r_1)\phi_{1s}(r_2)\right]\\ & \ \ \ \ |(\mathcal{H}_1 + \mathcal{H}_2 + \mathcal{H}_{12})|\left[\phi_{1s}(r_1)\phi_{2s}(r_2) \pm \phi_{2s}(r_1)\phi_{1s}(r_2)\right]>\end{aligned}$

The energy can be calculated with the expectation value of the wave function, which is a function of electron 1 and electron 2, with the Hamiltonian that we wrote down before. Do remember that $\mathcal{H}_1$ only operates on wave functions of electron 1, similarly for $\mathcal{H}_2$ , while $\mathcal{H}_{12}$ operates on the parts of both electron 1 and 2.

To go from the first to the second line, we implemented the form of the wave function from before, with plus for the symmetric case and minus for the anti-symmetric case of the spatial wave function. The next step will be to work them all out, which gives the lengthy equation shown below:

$\begin{aligned}E & = \frac{1}{2}\left[<\phi_{1s}(r_1)|\mathcal{H}_1|\phi_{2s}(r_1)> + <\phi_{2s}(r_1)|\mathcal{H}_1|\phi_{1s}(r_1)>\\ & \ \ \ \ +<\left[\phi_{1s}(r_2)|\mathcal{H}_2|\phi_{2s}(r_2)> + <\phi_{2s}(r_2)|\mathcal{H}_2|\phi_{2s}(r_2)>\\ & \ \ \ \ +<\phi_{1s}(r_1)\phi_{2s}(r_2)|\mathcal{H}_{12}|\phi_{1s}(r_1)\phi_{2s}(r_2)>\\ & \ \ \ \ +<\phi_{2s}(r_1)\phi_{1s}(r_2)|\mathcal{H}_{12}|\phi_{2s}(r_1)\phi_{1s}(r_2)>\\ & \ \ \ \ \pm<\phi_{1s}(r_1)\phi_{2s}(r_2)|\mathcal{H}_{12}|\phi_{2s}(r_1)\phi_{1s}(r_2)>\\ & \ \ \ \ \pm<\phi_{2s}(r_1)\phi_{1s}(r_2)|\mathcal{H}_{12}|\phi_{1s}(r_1)\phi_{2s}(r_2)>\end{aligned}$

In the first row we have a term with electron 1 and the $1s$ orbital, and a second term with electron 1 and the $2s$ orbital. What this describes is the energy of electron 1 in the $1s$ orbital plus the energy of electron 1 in the $2s$ orbital. We will call this $E_1$ .
In the second row, it is similar, but now it is for electron 2. This is the energy of electron 2 in the $1s$ orbital plus the energy of electron 2 in the $2s$ orbital. We call this $E_2$ . Since the electrons are indistinguishable, it will be the same energy as for the first electron.
In the first term (line 3), we have electron 1 in orbital $1s$ and electron 2 in $2s$ , with the Coulomb interaction operator. In the second term (line 4), we have electron 1 in the $2s$ orbital and electron 2 in the $1s$ orbital. We call both terms, $K$ . So far all the signs have been positive, which changes in the last term.
here we notice the $\pm$ , where it is positive when we have a symmetric spatial form of the wave function and negative for the anti-symmetric spatial form. This is exactly what is going to change the relative energies of the two wave functions. In the first term (line 5) you see electron 1 in the $1s$ orbital and electron 2 in the $2s$ orbital, times the coulomb interaction, and we see that now electron 1 is in the $2s$ orbital and electron 2 in the $1s$ . That means we have exchanged the orbital that each electron is sitting in. Likewise in line 6, we have done the same, but where electron 1 starts in $2s$ and electron 2 starts in $1s$ . We call these terms $J$

We can shorten the equation to look like:

$E = E_1 + E_2 + K \pm J$

where + is for the symmetric spatial part, thus anti-parallel spins ( $\uparrow\downarrow$ ); and – is for the anti-symmetric spatial part, and parallel spins ( $\uparrow\uparrow$ ).

3.1 Coulomb interaction

The expression for $K$ is

$\begin{aligned}K & =\ <\phi_{1s}(r_1)\phi_{2s}(r_2)|\mathcal{H}_{12}|\phi_{1s}(r_1)\phi_{2s}(r_2)>\\ & \ \ \ \ +<\phi_{2s}(r_1)\phi_{1s}(r_2)|\mathcal{H}_{12}|\phi_{2s}(r_1)\phi_{1s}(r_2)>\end{aligned}$

where $\mathcal{H}_{12}$ represents the Coulomb interaction between two electrons, as described above. The Coulomb interaction integral can be written as:

$\begin{aligned}K=\int\phi_{1s}^{*}(r_1)\phi_{1s}(r_1)\frac{e^2}{4\pi\varepsilon_0r_{12}}\phi_{2s}^{*}(r_2)\phi_{2s}(r_2)dV_1dV_2\\ &+\int\phi_{2s}^{*}(r_1)\phi_{2s}(r_1)\frac{e^2}{4\pi\varepsilon_0r_{12}}\phi_{1s}^{*}(r_2)\phi_{1s}(r_2)dV_1dV_2\end{aligned}$

The complex conjugate and the real part can be rewritten as the square modulus of the electronic wave function squared. We can further simplify this equation, by defining the charge densities:

$\rho_{1s}(r_1) = |\phi_{1s}(r_1)|^2\ \ \text{and}\ \ \rho_{2s}(r_2) = |\phi_{2s}(r_2)|^2$

The integral then further simplifies to:

$\begin{aligned}K & = \int\rho_{1s}(r_1)\frac{e^2}{4\pi\varepsilon_0r_{12}}\rho_{2s}(r_2)dV_1dV_2\\ & \ \ \ \ +\int\rho_{2s}(r_1)\frac{e^2}{4\pi\varepsilon_0r_{12}}\rho_{1s}(r_2)dV_1dV_2\end{aligned}$

This integral $K$ represents the total Coulomb interaction between the charge densities of electrons in the $1s$ orbitals. The positive sign correctly indicates that this is the sum of the Coulomb interactions from both possible configurations (electron 1 in the $1s$ orbital and electron 2 in the $2s$ orbital, plus electron 1 in the $2s$ orbital and electron 2 in the $1s$ orbital).

So, these terms in $K$ represent the quantum mechanical exact analog to the classical coulomb interaction between two charge distributions.

3.2 Exchange interaction

The expression for $J$ is:

$\begin{aligned}J & =\ <\phi_{1s}(r_1)\phi_{2s}(r_2)|\mathcal{H}_{12}|\phi_{2s}(r_1)\phi_{1s}(r_2)>\\ & \ \ \ \ \pm<\phi_{2s}(r_1)\phi_{1s}(r_2)|\mathcal{H}_{12}|\phi_{1s}(r_1)\phi_{2s}(r_2)>\end{aligned}$

In this expression, the interaction remains the Coulomb interaction between the two electrons, but with their spatial coordinates exchanged between the orbitals. The key point here is that this term cannot be expressed in terms of charge densities because the orbital of each electron on the left side of the inner product differs from the orbital on the right side. For example, in the first term, electron 1 is in the $1s$ orbital on the left but in the $2s$ orbital on the right. The same applies to electron 2.

This type of interaction is purely quantum mechanical and has no classical analog. It is known as the exchange interaction and arises due to the indistinguishable nature of electrons and the requirement that the total wavefunction (spatial part multiplied by the spin part) be antisymmetric under the exchange of two electrons.

4. The result

The exchange interaction plays a crucial role in determining the energy of different spin states:

Symmetric Spatial Wave Function (Anti-Parallel Spins, $\uparrow\downarrow$ ):
When the spatial part of the wavefunction is symmetric, the spin part must be anti-symmetric, corresponding to anti-parallel spins. The energy associated with this configuration is higher because the symmetric spatial wavefunction increases the overlap between electron wavefunctions, leading to greater Coulomb repulsion.
Anti-Symmetric Spatial Wave Function (Parallel Spins, $\uparrow\uparrow$ ):
When the spatial part of the wavefunction is anti-symmetric, the spin part must be symmetric, corresponding to parallel spins. This configuration reduces the overlap between the electron wavefunctions, resulting in lower Coulomb repulsion and, consequently, a lower energy.

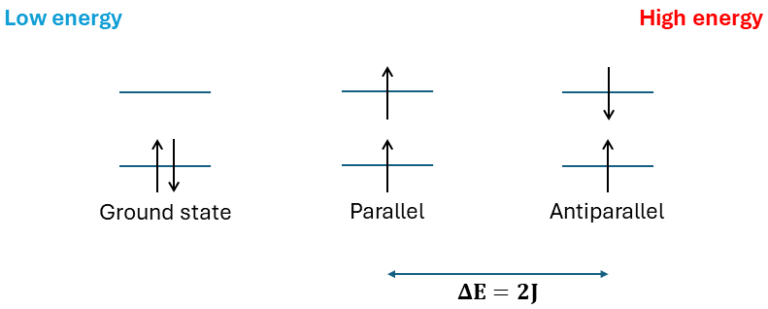
As a result, the energy of the symmetric spatial wavefunction (anti-parallel spins) is higher by an amount $2J$ than that of the anti-symmetric spatial wavefunction (parallel spins). The arrangement of parallel spins (with a net magnetic moment) typically corresponds to a lower energy state because of the reduced repulsion.

As a side note, in Helium, the ground state is non-magnetic, as both electrons occupy the $1s$ orbital and pair up with anti-parallel spins, forming a singlet state. This singlet state has the lowest energy due to the complete filling of the $1s$ orbital and the minimized electron repulsion in this configuration.

WE’ve now seen the exchange interaction in a single atom, but it is also used to explain ferromagnetism. Read more on this topic on my article on the basics of ferromagnetism.

Post Views: 56

0 0 votes

Article Rating

0 Comments

Oldest

Newest Most Voted

Inline Feedbacks

View all comments