Updated 3 July 2024

Published 15 June 2024

The Bohr atom model

1. Earlier discoveries

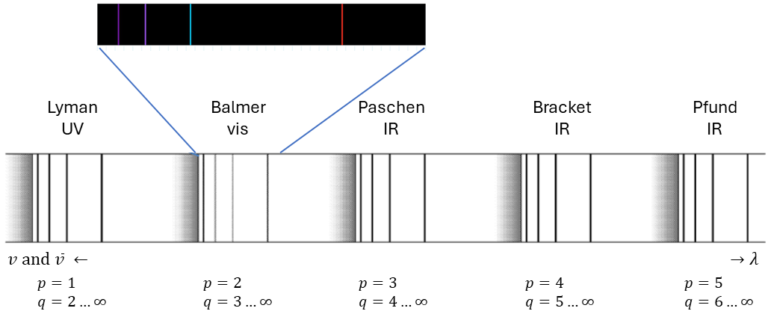
1.1 Hydrogen spectrum and the Balmer series

In atomic physics, one of the fundamental observations involves the spectral lines emitted by hydrogen atoms [1]. These lines are not random but follow a specific pattern that can be described using the Rydberg formula, discovered empirically in 1888. This regular structure indicates that the electrons in a hydrogen atom occupy certain fixed energy states. But why do these electrons behave this way? Niels Bohr provided the first explanation through his hydrogen model.

The Balmer series is a set of spectral lines emitted by the hydrogen atom. In 1885, Johann Balmer discovered an empirical formula to calculate these lines [3]:

$\bar{v} = \frac{1}{\lambda} = R_H\right[\frac{1}{p^2}-\frac{1}{q^2}\right]$

where $\bar{v} = 1/\lambda =v/c$ is the wavenumber, $v$ is the frequency, $c$ is the speed of light, and $R_H$ is the Rydberg constant, $1.096758\times 10^{7} m^{-1}$ The formula shows that the spectral lines can be predicted by knowing the values of $p$ and $q$ , which are integers with $q>p$ . This discovery was crucial in understanding the quantized nature of atomic energy levels.

1.2 Blackbody radiation

The other important discovery, was the solution to the blackbody radiation problem. Blackbody radiation is the thermal electromagnetic radiation within or surrounding a body in thermodynamic equilibrium. This radiation has a characteristic spectrum that depends solely on the body’s temperature. According to classical theories, the number of electromagnetic modes within the body is proportional to the square of the frequency.

The Rayleigh-Jeans law, a classical description, states that the radiance of blackbody radiation is proportional to the inverse square of the wavelength. This law works well for long wavelengths but fails for short wavelengths. As the wavelength decreases, the predicted intensity increases without bounds, leading to the so-called “ultraviolet catastrophe.”

The paradox was resolved by Max Planck in 1901. Planck proposed that the energy emitted by a blackbody is not continuous but quantized. The energy of each mode with frequency $v$ is given by $E=nhv$ where $n$ is an integer ( $0, 1, 2, …$ ), and $h$ is Planck’s constant ( $6.626\times 10^{-34} J s$ ). This quantization means that higher frequency modes require more energy to be excited, reducing the probability that these modes will be excited (hence it the radiance drops to near zero the UV part of Figure 2). With this assumption, Planck was able to describe the intensity distribution of blackbody radiation accurately, which classical physics could not explain [4].

1.3 From Planck to Bohr

In 1913, Niels Bohr used Planck’s idea to propose a solution to the ‘crashing planet’ problem associated with the classical model of electrons orbiting the nucleus. According to classical physics, electrons should continuously lose energy as they orbit the nucleus, eventually spiraling inward and collapsing into the nucleus.

Bohr suggested that:

Electrons cannot lose energy continuously because Planck showed that energy is emitted in discrete packages (quanta).
If these energy packages are similar in magnitude to the energy levels of electrons in the atom, then electrons can only emit or absorb these discrete packages when changing orbits. Alternatively, for some reason, they might be hindered from doing so and therefore remain in their orbits.

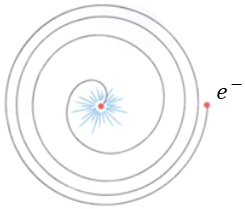
2. Bohr Radius, and energy

2.1 The three postulates

To update Rutherford’s model of a nucleus with electrons around it (without a specific orbit), Niels Bohr came up with three postulates (axioms or assumptions), that could describe his model, that was primarily based on the emission spectra of hydrogen. The following three postulates were stated [2]:

There are relatively stable states for an electron in an atom in which it can stay without emitting energy (the lowest state is absolutely stable).
An electron can jump between two of these states by absorbing or emitting radiation of an energy equal to the difference between the two states (using Planck’s definition of discrete energy values).
The frequency of the radiation is equal to the frequency with which the electron circulates with velocity and a radial distance around the nucleus. (The third postulate was later re-formulated by Bohr as: Energetic states of the electron are possible for which the total angular momentum $L = mvr$ of the atom is a multiple of the Planck constant $\hbar$ , so $L=nh/2\pi = n\hbar$ ).

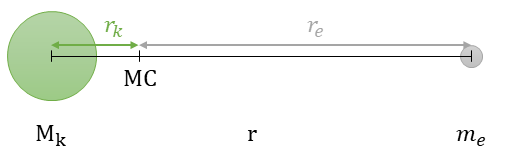
A closer look at the third postulate, we know the following by looking at Figure 3:

The nucleus and the electron revolve around their common center of mass ( $MC$ ) with the same angular velocity $\omega = v\r$ .
The centripetal forces $F = mr\omega^2$ acting on the nucleus and electron are equal in magnitude. Thus, $M_kr_k = m_er_e$ .
and with this the distances between $MC$ and nucleus $r_k= rm_e/(M_k+m_e)$ and $MC$ and electron $r_e = rM_k/(M_k+m_e)$ can be calculated.

By inserting all the above into the third postulate and using the concept of effective mass $\mu = m_eM_k/(M_k+m_e)$ , the third postulate simplifies to:

$\mu v r = n\frac{h}{2\pi}$

2.2 The Bohr Radius

For a stable orbit, the Coulomb attraction force ( $\frac{Ze^2}{4\pi\varepsilon_0 r^2}$ ) between the nucleus with $Z$ elementary charges and the electron with one elementary charge provides the necessary centripetal force ( $\frac{\mu v^2}{r}$ ) to keep the electron in orbit.

$\frac{Ze^2}{4\pi\varepsilon_0r^2}=\frac{\mu v^2}{r}$

where $Z$ is the atom number (number of positive charges in the nucleus), $e = 1.602176\times10^{-19} C$ is the elementary charge, and $\varepsilon_0 = 8.8854187\times 10^{-12} F/m$ is the vacuum permittivity.

Using the third postulate $L=\mu vr = n\hbar$ , we can solve for the radius:

$r_n=\frac{\varepsilon_0h^2n^2}{\pi\mue^2Z}=\frac{n^2}{Z}r_1 = \frac{n^2}{Z}0.05292 nm$

For the hydrogen atom, with only one charge in the nucleus ( $Z=1$ ), and only 1 shell ( $n=1$ ), the radius $r=0.05292 nm$ equals the distance between the nucleus and the electron in a hydrogen atom in its ground state, and is also called the Bohr radius.

The ionization energy of the hydrogen atom ( $Z=1$ ) can be evaluated in the Bohr model which predicts that the atomic energy level $n$ has energy:

$E_n = -\frac{\mu e^4 Z^2}{8\varepsilon_0^2 h^2 n^2} = \frac{Z^2}{n^2}E_1 = (-13.595 eV)\frac{Z^2}{n^2}$

The energy $E=+13.595 eV = 1312 kJ/mol = 2.18\times 10^{-18} J/atom$ is the first ionization energy of the hydrogen atom (that is required to remove this electron from the atom). Energies of electrons are often given as electronvolts (eV). This is the amount of energy gained by the charge of a single electron moving across an electric potential difference of one volt. Thus it is 1 volt (1 joule per coulomb, 1 J/C) multiplied by the elementary charge, $e = 1.6021766208\times 10^{-19} C$ . Therefore, one electronvolt is equal to $1.6021766208 \times 10^{-19} J$ .

3. The Bohr model

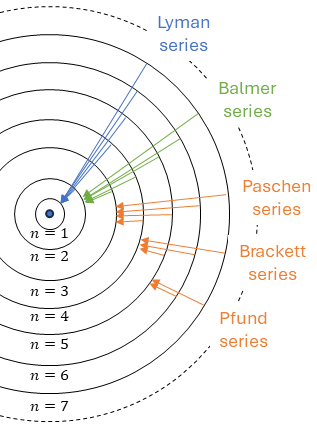
With this knowledge, we can calculate the energy levels of the emission spectroscopy of a hydrogen atom. We know that from the second postulate it follows that the energy of the emitted radiation must be the difference between the energy levels of two Bohr orbits.

$E_\textrm{emitted}=hv_\textrm{emitted} = E_i - E_f\ \ \rightarrow\ \bar{v}_\textrm{emitted} = \frac{v_\textrm{emitted}}{c}=-\frac{E_f-E_i}{hc}$

With the energy states calculated in the previous section (ionization energy $E_n$ ), and the reduced mass ( $\mu$ ), one obtains

$\bar{v}_\textrm{emitted} = \frac{m_ee^4}{8\varepsilon_0^2 h^3 c}\frac{M_k}{M_k+m_e}\cdot Z^2\cdot\left[\frac{1}{n_f^2}-\frac{1}{n_i^2}\right]$

where the first part of the right hand side can be summed up into $R_Z = 1.0973732 m^{-1}$ , which is close to the empirical solution of Rydberg (see first section).

Atoms with heavier nuclei and 1 electron ( $He^{+}, Li^{2+}, Be^{3+} …$ ) will have similar lines spectra, but $R_Z$ will be larger then $R_H$ (and $Z>1$ ) and the wavelengths will therefore be shorter. This is the so-called violet-shift.

Side note: If expressed in energies, instead of wavenumbers:

$E_\textrm{emitted} = hcR_Z Z^2\left[\frac{1}{n_f^2}-\frac{1}{n_i^2}\right]$

3.1 Disadvantages of the Bohr model

The three postulates that Bohr used for his theory are not proven, eventhough they fit the observations nicely.
Line splitting remains unexplained (high resolution spectroscopy shows that the single lines in the H-spectrum actually consist of 2 or more lines)
The spectra of multiple electron atoms cannot be explained
Also, Bohr assumes that during a quantum jump a discrete amount of energy is radiated. However, Bohr stuck to the classical Maxwell theory of the wave character of electromagnetic field. Quantization of the electromagnetic field was explained by the discreteness of the atomic energy levels; Bohr did not believe in the existence of photons. This made it difficult to explain another strange observation of electrons and the energy required to ionize them: the Photoelectric Effect

4. References

[1] Rydberg, J.R. . “On the structure of the line-spectra of the chemical elements”. Philosophical Magazine. 5th series, vol. 29, pp. 331–337 (1890)

[2] Bohr, N. “I. On the constitution of atoms and molecules”. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 26 (151): 1–25, 1913. doi:10.1080/14786441308634955.

[3] Bohr, Niels . “Niels Bohr – Session III” (Interview). Interviewed by Thomas S. Kuhn; Leon Rosenfeld; Aage Petersen; Erik Rudinger. American Institute of Physics, 1962.

[4] Kragh, H. “Max Planck: the reluctant revolutionary”. Physics World. 13 (12): 31–36 (2000). doi:10.1088/2058-7058/13/12/34.

Post Views: 5

0 0 votes

Article Rating

0 Comments

Inline Feedbacks

View all comments