Updated 7 July 2024

Published 25 June 2024

An introduction to Skyrmions

1. Introduction

Skyrmions are a class of topological solitons discovered by Tony Skyrme in the 1960s. He used this concept to describe how subatomic particles exist as discrete entities in a nuclear field. The original idea was overshadowed by other theories; however, the same concept is now used to describe a phenomenon in condensed matter physics. These topological solitons can be understood as a singularity or some kind of knot in a vector field that cannot be unwound or annihilated.

The original concept of Skyrme was extended to magnetism in 1989, by Bogdanov and Yablonskii [1]. They modeled that a lattice of vortices in magnets is thermodynamically stable at zero temperature. In the years after, Bogdanov and Hubert [2] did more research on the phase boundary between this skyrmion lattice and the helical phase and predicted a stable phase of isolated skyrmions. It took until 2006 before the term $skyrmion$ was mentioned by Rössler, Pfleiderer and Bogdanov [3], who proved that the skyrmion lattice phase is one of the several possible ground states in chiral magnets.

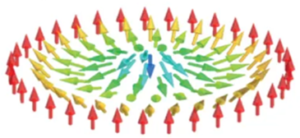
A magnetic skyrmion can be visualized by a point of reversed magnetization in a ferromagnetic state. The finite radius where the magnetization gradually turns between the two reversed states is shown in Figure 1. In this case, the ferromagnet has its spins uniformly oriented up, while the singularity in the skyrmion is pointing down. There are different configurations of how the magnetization vector rotates from its center to the uniform ferromagnet state. The main two types of skyrmions are the Bloch skyrmion and the Néel skyrmion.

The Bloch skyrmion, also known as the ‘vortex’ configuration, has its magnetization rotate perpendicular to the plane between the two opposite magnetizations. Due to the bulk-DM interaction, Bloch skyrmions mainly exist in bulk materiasl.
The Néel skyrmion, also referred to as the ‘spiky’ configuration, has its magnetization rotate parallel to the plane between the opposite magnetizations. Due to the interfacial-DM interaction, Néel skyrmions are more stable in thin film ferromagnets.

2. Skyrmion properties & stabilization

In this section, we delve into the fascinating world of skyrmions, exploring their unique topological properties and the factors that contribute to their stability. Skyrmions are nanoscale, vortex-like spin structures that exhibit remarkable stability due to their topological nature. These quasi-particles have garnered significant attention in the field of condensed matter physics and spintronics for their potential applications in next-generation data storage and processing technologies. Understanding the topological characteristics and stabilization mechanisms of skyrmions is crucial for harnessing their properties for practical use.

2.1 Topology

The stability of magnetic skyrmions is linked to the topological configuration of the vector field of the magnetization. In mathematics, topology is the study of geometric properties that remain unchanged under continuous deformation (i.e. stretching, molding), without tearing. An example of two topologically equivalent shapes is given in Figure 2. The coffee mug can be deformed and molded into a donut. This transformation can be done without tearing anything or extruding more holes in the shape; therefore, these two shapes are topologically equivalent.

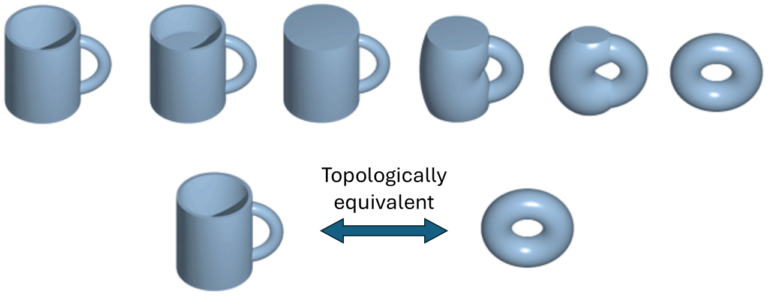
The idea is that the shape of the skyrmion is topologically different from the uniform magnetization of the ferromagnet. Therefore, they are topologically inequivalent geometries that cannot be continuously deformed, which hence provides additional stability to the geometry.

In the context of 2D and quasi-2D systems, the topological structure of a spin texture is generally characterized by the topological charge [55-57], which is also referred to as the Pontryagin number [2, 3]:

$Q = \frac{1}{4\pi}\int d^2\textbf{r}\cdot \textbf{m}(\textbf{r})\cdot (\partial_x \textbf{m}(\textbf{r})\times\partial_y \textbf{m}(\textbf{r}))$

For example, as shown in Figure 1, the Bloch-type and Néel-type skyrmions have topological charges of $Q = -1$ (for the center magnetization of $-m_z$ ), while the antiskyrmion of the same center magnetization, has the opposite topological charge ( $Q = +1$ ). There is in fact a whole zoo of skyrmion-like spin textures.

Chiral magnetic skyrmions are not just limited to a topological charge of $\mid Q\mid = 1$ , and can be of any topological charge. As an example, a skyrmionium can be considered a combination of a skyrmion with $Q = +1$ and a skyrmion with $Q = -1$ , resulting in a topological charge of $Q = 0$ . Another example is the biskyrmion, with a topological charge of $Q = -2$ , which can form in chiral bulk or frustrated magnets when two skyrmions with a topological charge of $Q = -1$ approach each other. Furthermore, there are other configurations, such as the meron and bimeron, with a topological charge of $Q = -0.5$ and $Q = -1$ , respectively.

As there are so many topological spin textures, they cannot be fully distinguished using only the topological charge $Q$ , as there could be some degenerate states for the same charge. Therefore, you can also calculate the vorticity number $Q_v$ and the helicity number $Q_h$ , which completely characterize all the different skyrmions. For this, the term $\textbf{m}(\textbf{r})$ can be rewritten in terms of out-of-plane ( $\theta$ ) and in-plane spin ( $\phi$ ) textures:

$\textbf{m}(\theta, \phi) = \left[\textrm{sin}\theta\textrm{cos}(Q_v\phi + Q_h),\ \textrm{sin}\theta\textrm{sin}(Q_v\phi + Q_h),\ \textrm{cos}\theta\right]$

These topological spin textures with different topological structures constitute a large family and lead to the emerging field of topological magnetism, which promises new opportunities for magnetic and spintronic applications.

The bulk DM interaction could result in the stabilization of Bloch-type skyrmions with $(Q = +1, Q_v = +1, \mid Q_h\mid = \pi/2)$ and $(Q = -1, Q_v = +1, \mid Q_h\mid = \pi/2)$ .
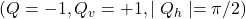The interfacial DM interaction could result in the stabilization of Néel-type skyrmions with 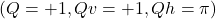$(Q = +1, Qv = +1, Qh = \pi)$ and $(Q = -1, Qv = +1, Qh = 0)$ .

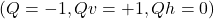2.2 Stability & Magnetic phase diagrams

The stability of the skyrmion also depends on external factors. In 2009, Mühlbauer et al [4] measured the magnetic phase diagram (B-T) of MnSi, as shown in Figure 4. The key findings of their paper for this particular material are:

Helical magnetic order develops below a critical temperature ( 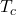$T_c$ ) in the absence of a magnetic field ( $B = 0$ ). This means that the spins of the electrons in the material order in a helical pattern.
The helical order unpins and aligns along the applied magnetic field ( 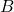$B$ ) above a critical field 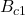$B_{c1}$ . This indicates that the helical pattern straightens out and follows the direction of the applied field when the field is strong enough.
For even higher magnetic fields ( $B > B_{c2}$ ), the helical modulation collapses, and the spins become aligned in the direction of the field (ferromagnetic state). This suggests that a very strong field overcomes the intrinsic tendency of the spins to form a helical pattern and forces them to align entirely.
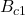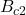In a finite field window between $B_{c1}$ and $B_{c2}$ , a new magnetic phase called the A-phase emerges. This phase is characterized by a sixfold symmetric arrangement of Bragg reflections in neutron scattering data, indicating a complex magnetic structure.

The paper proposes that the A phase is a skyrmion lattice, a crystal-like structure formed by topologically stable magnetic swirls called skyrmions. These skyrmions are thought to be stabilized by thermal fluctuations in the system. As is clear from the figure, the window in which the skyrmion lattice can exist and be stable is quite narrow, and requires tuning of your system to stabilize it.

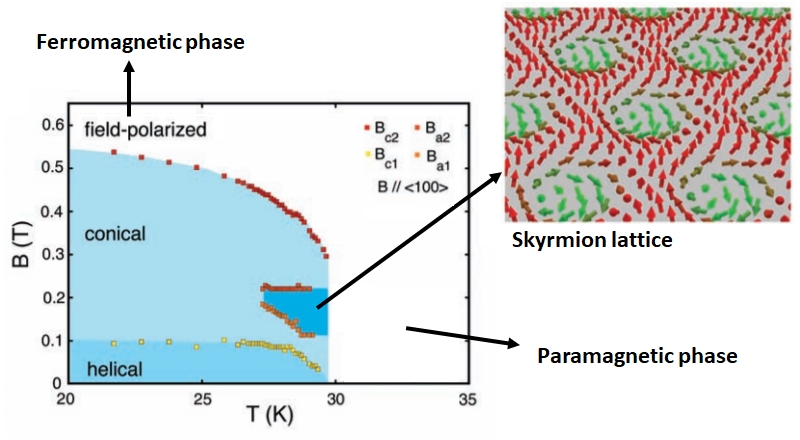
After the first observation in MnSi [4], several more experiments on other materials showed these phases. First, only in bulk materials, but later on as well in thin films where the skyrmion lattice phase extended to lower temperatures [5]. Instead of thinning down a bulk material into a thin film, a different approach is to grow ferromagnetic material on a heavy metal layer [6]. Table 1 gives an overview of a few discovered materials, some of which have a stable skyrmion phase up to room temperature.

Thin films and bulk materials have different material properties, such as the Dzyaloshinskii-Moriya interaction (DMI) [7][8], exchange interaction, and anisotropy, that allow skyrmions to form. In bulk materials, the DMI is induced by the spin-orbit coupling combined with the absence of inversion symmetry due to the non-centrosymmetrical (chiral) crystal lattice [9]. In the case of the interface between a ferromagnet and a metal, the broken inversion symmetry happens at this interface between the two materials. Because of the strong spin-orbit coupling at the interface, it generates a different kind of DMI, namely the interfacial DMI [10].

Table 1: A selection of different materials that host skyrmion lattices. The table has bulk materials, thin films and multi-layered materials. The complete table can be found at [25].

Material	Sample	Conduction	$T_C$	Type
MnSi	Bulk	Metal	28-29.5	Block
MnSi	Film (50nm)	metal	<5-23	Bloch
FeGe	Bulk	metal	273-278	Bloch
FeGe	Film (15nm)	Metal	60-280	Bloch
Cu2OSeO2	Bulk	Insulator	56-58	Bloch
Fe/Ir(111)	Trilayer	metal	8	Neel
(Ir/Co/Pt)10	Multilayer	Metal	300	Neel
Pt/Co/Ta	Multilayer	Metal	300	Neel
W/Co20/Fe60/B20/MgO	Multilayer	Metal	300	Neel

In both bulk materials and thin films, it is observed that the spin at the center of the skyrmion is pointing in the opposite direction from the spins along the edge; this direction depends on the external applied field on the ferromagnetic material. This transition from the magnetization direction of the central spin to the edge is characterized by two different variants, namely the Néel skyrmion (Fig 2.a) and Bloch skyrmion (Fig 2.b). Normally, due to the slightly different mechanics, the interfacial materials can stabilize the Néel variant [11], while Bloch skyrmions are typically seen in bulk ferromagnets, as shown in Table 1.

3. Future application of skyrmion

The introduction of computer technology was without a doubt one of the biggest changes in the last century. Nowadays, almost every device has integrated circuitry that enables many different functions. One component that is required in almost every device is memory. There is a large variety of different memories that satisfy specific needs; they are characterized by their storage capacity, reading and writing speeds, physical size, endurance , and more.

One of the older options of storing digital information is the magnetic Hard Disk Drives (HDDs). Although the cost of storing information is low, it is inherently slow with typical reading and writing speeds in the order of milliseconds due to mechanical moving parts. The part of the HDD for storage consists of a material that has a high magneto-crystalline anisotropy with two local energetic minima, which can be considered as the two opposite orientations of the magnetic moment of the ferromagnetic [13][14]. These two ferromagnetic states are protected by their respective energy barriers and because of that they have a very long lifetime. This ground state and its opposite state can be utilized as a single bit, which can be read out by the giant magneto resistance effect [15][16], which gives a change in the resistance depending on the domain’s orientation. To write a single bit, a large magnetic field can reorientate the specific domain [17].

In the case of the HDD, either the head or the storage medium itself has to move to address each domain separately. This adds significant delay to the whole process and also limits scaling down these mechanical devices. For these reasons, new and innovative ideas have been proposed to replace the existing HDDs. In recent years, Flash memory has slowly replaced all HDDs and due to its 3D architecture, it can achieve high-density non-volatile memory. In 2004, S. S. P. Parking et al. [18] conceptualized an alternative 3D idea, called the racetrack memory. The information is stored in magnetic domains and to maximize the storage density, these tracks are formed in tall columns, perpendicular to the surface. Each of these magnetic domains is separated by domain walls (DW) that act as the boundaries. The length between consecutive DWs is determined by specific pinning sites along the strip, that also give the DWs a certain stability against fluctuations [18].

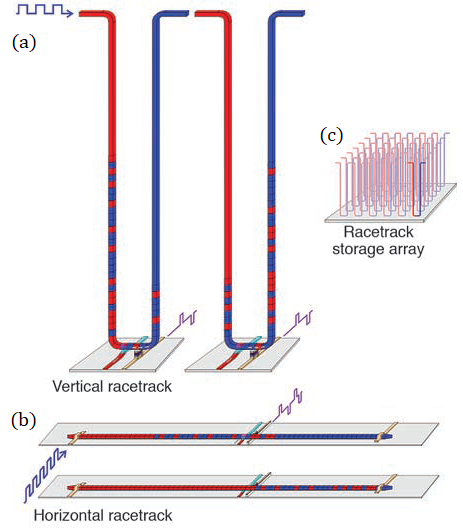
Figure 4(a) shows such a vertical racetrack memory, which can be considered as a shift register on which the DWs move from left to right (or vice versa) along the track by applying a pulsed current. This current will get spin polarized by the magnetic material and by conservation of momentum, the angular momentum of the spin is transferred to the domains, by a phenomenon called spin transfer torque (STT). Furthermore, a static read- or write-head can target specific domains that pass by [19].

However, several challenges have to be tackled such as reducing the critical current that is required to move the DW, while keeping a velocity of 10-100 m/s. Another downside of using DWs is that they can get pinned on defects. These detrimental effects need to be overcome to make it competitive with alternative existing memories. The fact that skyrmions can have a small size [20] and they do not require large critical currents to move, makes them potential candidates for a replacement of DWs as binary bits. Another useful property of skyrmions is that they are topologically protected, allowing them to pass by defects without getting pinned. Fert et al. [21] also show that even though the relation between velocity and applied current is not different from domain walls, they are able to move at lower currents. With the skyrmion size of 10 nm [20], it is smaller than a DW and it allows for higher information access speed and higher density. Alternatively, similar access speed as DW can be achieved with lower currents, which leads to lower energy consumption. The binary information that is encoded in spin up and down for the DW racetrack memory has to be rfeplaced by the topological number of skyrmions. Readout could be performed by measuring the Hall effect and writing can be done by annihilating the skyrmion to obtain a binary ‘0’ and nucleating a skyrmion for a binary ‘1’ [19].

The main issue nowadays is detecting and creating these skyrmions. This is the reason why a lot of research is done in the detection [22][23][24] and the creation of new skyrmions, the latter will be explained in more detail in the next chapter.

4. References

[1] A. N. Bogdanov and D. A. Yablonskii, Thermodynamically stable “vortices” in magnetically ordered crystals. The mixed state of magnets, Journal of Experimental and Theoretical Physics, vol. 68, 101, (1989).

[2] A. N. Bogdanov and A. Hubert, Thermodynamically stable magnetic vortex states in magnetic crystals, Journal of Magnetism and Magnetic Materials, vol. 138, pp. 255-269, (1994).

[3] U. K. Rössler and A. N. Bogdanov and C. Pfleiderer, Spontaneous skyrmion ground states in magnetic metals, Nature, vol. 442, pp. 797-801, (2006).

[4] S. Muhlbauer et al., Skyrmion Lattice in a Chiral Magnet, Science, vol. 13, pp. 915-919, (2009)

[5] X. Z. Yu and Y. Onose et al., Real-space observation of a two-dimensional skyrmion crystal, Nature, vol. 465, pp. 901-904, (2010).

[6] M. Bode and M. Heide et al., Chiral magnetic order at surfaces driven by inversion asymmetry, Nature, vol. 447, pp. 190-193, (2007).

[7] I. Dzyaloshinsky, A thermodynamic theory of weak ferromagnetism of antiferromagnetics, J. Phys. Chem. Solids, vol. 4, pp. 241-255, (1958).

[8] T. Moriya, New mechanism of anysotropic superexchange interaction, Physical review letters, vol. 4, 5, (1960).

[9] A. Fert and N. Reyren and V. Cros, Magnetic skyrmions: advances in physics and potential applications, Nature Review materials, vol. 2, pp. 1-15, 17031, (2017).

[10] S. Heinze and K. von Bergmann et al., Spontaneous atomic-scale magnetic skyrmion lattice in two dimensions, Nature Physics, vol. 7, pp. 713-718, (2011).

[11] F. Tejo et al., Distinct magnetic field dependence of Neel skyrmion sizes in ultrathin nanodots, Scientific Reports, vol. 8, 6280, (2018).

[12] L. Kish, Skyrmions in Chiral Magnets, Lecture at the University of Illinois at Urbana-Champaign, Available: http://guava.physics.uiuc.edu/~nigel/courses/569/Essays_Spring2018/Files/kish.pdf

[13] N. Tsukahara et al., Adsorption-Induced Switching of Magnetic Anisotropy in a Single Iron(II) Phthalocyanine Molecule on an Oxidized Cu(110) Surface, Phys. Rev. Lett., vol. 102, 167203, (2009).

[14] C. F. Hirjibehedin et al., Large Magnetic Anisotropy of a Single Atomic Spin Embedded in a Surface Molecular Network, Science, vol. 317, 5842, (2007).

[15] M. N. Baibich et al, Giant Magnetoresistance of (001)Fe/(001)Cr Magnetic Superlattices, Phys. Rev. Lett., vol. 61, 2472, (1988).

[16] S. S. P. Parkin et al., Oscillations in exchange coupling and magnetoresistance in metallic superlattice structures: Co/Ru, Co/Cr, and Fe/Cr, Phys. Rev. Lett., vol. 64, 2304, (1990).

[17] G. Binasch et al., Enhanced magnetoresistance in layered magnetic structures with antiferromagnetic interlayer exchange, Phys. rev. B, vol. 39, pp. 4828-4830, (1989).

[18] S. S. P. Parkin, M. Hayashi and L. Thomas, Magnetic Domain-Wall Racetrack Memory, Science, vol. 320, 190-194, (2008).

[19] S. Zhang et al., Topological computation based on direct magnetic logic communication, Sci. Rep., vol. 5, 15773, (2015).

[20] L. Caretta et al., Fast current-driven domain walls and small skyrmions in a compensated ferrimagnet, Nature Nanotech., vol. 13, pp. 1154-1160, (2018).

[21] A. Fert and V. Cros and J. Sampaio, Skyrmions on the track, Nature Nanotechnology, vol. 8, pp. 152-156, (2013).

[22] T. L. Monchesky, Detection with unpolarized currents, Nature Nanotech., vol. 10, pp. 1008-1009, (2015).

[23] C. Hanneken et al., Electrical detection of magnetic skyrmions by non-collinear magnetoresistance, Nature Nanotech., vol. 10, pp. 1039-1042, (2015).

[24] K. Hamamoto et al., Purely electrical detection of a skyrmion in constricted geometry, Appl. Phys. Lett., vol. 108, 112401, (2016).

[25] K. Everschor-Sitte et al., Perspective: Magnetic skyrmions-Overview of recent progress in an active research field, Journal of Applied Physics, vol. 124, 240901, (2018).

Post Views: 85

0 0 votes

Article Rating

0 Comments

Oldest

Newest Most Voted

Inline Feedbacks

View all comments